The principal classes of Dakota algorithms, with brief descriptions, are summarized here:

• Design optimization: Optimization solvers seek to minimize cost or maximize system performance, as predicted by the simulation model, subject to constraints on input variables or secondary simulation responses. Categories of algorithms include gradient-based, derivative-free, and global optimization. Dakota also includes capabilities for multi-objective trade-off optimization and automatic scaling of problem formulations. Advanced Dakota approaches include hybrid (multi-method), multi-start local, and Pareto-set optimization.
• Parameters estimation: Parameter studies employ deterministic designs to explore the effect of parametric changes within simulation models, yielding one form of sensitivity analysis. They can help assess simulation characteristics such as smoothness, multi-modality, robustness, and nonlinearity, which affect the choice of algorithms and controls in follow-on optimization and UQ studies. Typical examples include centered, one-at-a-time variations or joint variation on a grid.
• Uncertain quantification: Uncertainty quantification methods (also referred to as nondeterministic analysis methods) compute probabilistic information about response functions based on simulations performed according to specified input parameter probability distributions.
• Sensitivity analisys: formalizes and generalizes one-off sensitivity studies you are likely already doing

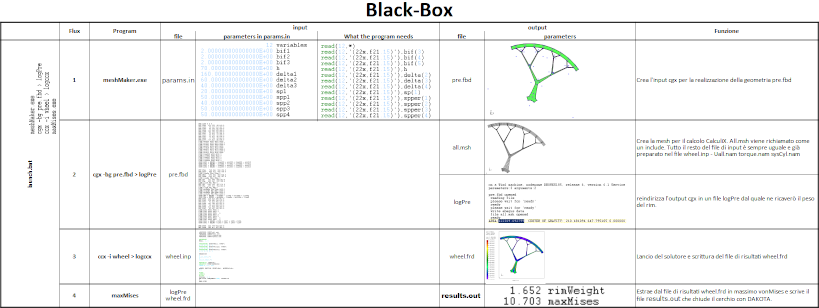
DAKOTA operates on an external solver like a black-box, as explained in the scheme below:

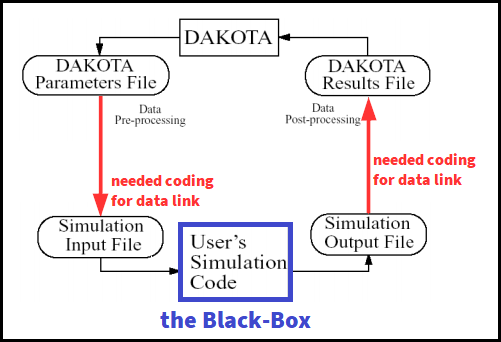
The two red arrows represent the required coding skills, which we can provide to facilitate the data linking between the solver and the DAKOTA algorithm.

Below an example of the black-box and the related implementation for the red arrows needed to link DAKOTA to the black-box as mentioned before: